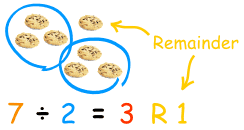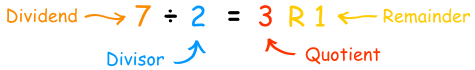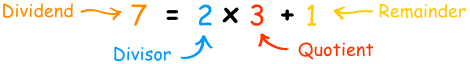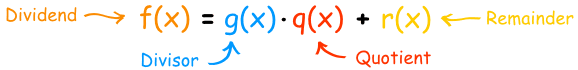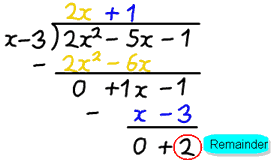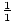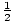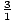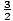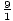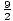3.3 - Real Zeros of Polynomial Functions
Long Division of Polynomials
You were taught long division of polynomials in Intermediate Algebra. Basically, the procedure is carried out like long division of real numbers. The procedure is explained in the textbook if you're not familiar with it.
One key point about division, and this works for real numbers as well as for polynomial division, needs to be pointed out. When you divide the dividend by the divisor, you get a quotient and a remainder. To check the problem, you multiply the divisor by the quotient and add the remainder to get the dividend. If the remainder is 0, then we say that the divisor divides evenly into the dividend.
Dividend / Divisor = Quotient + Remainder / Divisor
Dividend = Divisor * Quotient + Remainder
Like I said, the same thing can be done with polynomial functions.
f(x) = d(x) * q(x) + r(x)
Where f(x) is the polynomial function being divided into (dividend), d(x) is the polynomial function being divided by (divisor), q(x) is the polynomial function that is the quotient, and r(x) is the polynomial remainder function and will have degree less than the divisor.
If the remainder, r(x), is zero, then f(x) = d(x)*q(x). We have just factored the function f(x) into two factors, d(x) and q(x).
Remainder Theorem
When a polynomial function f is divided by x-k, the remainder r is f(k).
Okay, now in English. If you divide a polynomial by a linear factor, x-k, the remainder is the value you would get if you plugged x=k into the function and evaluated.
Now, tie that into what we just said above. If the remainder is zero, then you have successfully factored the polynomial. If the remainder when dividing by (x-k) is zero, then the function evaluated at x=k is zero and you have found a zero or root of the polynomial. Plus, you now have a factored polynomial (the quotient) which is one less degree than the original polynomial. If the quotient is down to a quadratic or linear factor, then you can solve and find the other solutions.
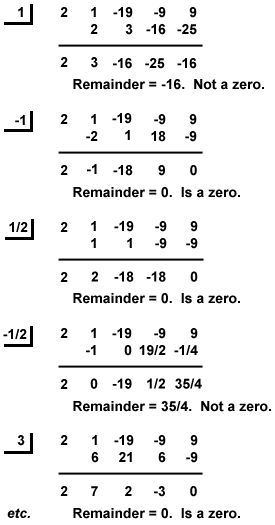
Synthetic Division
To divide a polynomial synthetically by x-k, perform the following steps.
Setup
- Write k down, leave some space after it.
- On the same line, right the coefficients of the polynomial function. Make sure you write the coefficients in order of decreasing power. Be sure to put a zero down if a power is missing. Place holders are very important
- For now, leave a blank line. Draw the left and bottom portions of a box. The left portion goes between the k and the coefficients. The bottom portion goes under the blank line you left.
Synthetic Division
Once you have things set up, you can actually start to perform the synthetic division.
- Bring the first coefficient down to the bottom row (below the line)
- Multiply the number in the bottom row by the constant k, and write the product in the next column of the second row (above the line).
- Add the numbers in the next column and write the total below the line.
- Repeat steps 2 and 3 until all the columns are filled.
Interpreting the Results
- The very last value is the remainder. If the remainder is zero, you have found a zero of the function.
- The rest of the values are the coefficients of the quotient. Each term will be raised to the one less power than the original dividend. (If it was a fourth degree polynomial to start with, the quotient will be a third degree polynomial).
Warnings
You can only use synthetic division as described above to divide by x-k. That is, it must be a linear factor, and the leading coefficient must be a one.
There are similar ways to divide by a quadratic, cubic, etc, but for some reason, they aren't taught anymore (no, they won't die with me, I'm sure someone else knows them, too, but thanks for your concern).
Fundamental Theorem of Algebra
Every polynomial in one variable of degree n, n > 0, has at least one real or complex zero.
Corollary to the Fundamental Theorem of Algebra
Every polynomial in one variable of degree n, n > 0, has exactly n real or complex zeros.
Complex Roots
Complex solutions come in pairs. If (a+bi) is a solution, then its complex conjugate (a-bi) is also a solution.
Square Roots
Solutions involving square roots also come in pairs. If a+sqrt(b) is a solution, then its conjugate, a-sqrt(b) will also be a solution. The same is not necessarily true of other roots.
Descartes' Rule of Signs
This is not in your text!
- The maximum number of positive real roots can be found by counting the number of sign changes in f(x). The actual number of positive real roots may be the maximum, or the maximum decreased by a multiple of two.
- The maximum number of negative real roots can be found by counting the number of sign changes in f(-x). The actual number of negative real roots may be the maximum, or the maximum decreased by a multiple of two.
- Complex roots always come in pairs. That's why the number of positive or number of negative roots must decrease by two.
Consider: f(x) = 3x^6 + x^5 - x^4 + 3x^3 + 2x^2 - x + 1.
The signs in f(x) are + + - + + - +. There are 4 sign changes (+ to -) or (- to +).
The signs in f(x) are + + - + + - +. There are 4 sign changes (+ to -) or (- to +).
Now, f(-x) = 3x^6 - x^5 - x^4 - 3x^3 + 2x^2 + x + 1.
The signs in f(-x) are + - - - + + +. There are 2 sign changes (+ to -) or (- to +).
The signs in f(-x) are + - - - + + +. There are 2 sign changes (+ to -) or (- to +).
Here are the Possible Combinations of Roots
| Total | Positive | Negative | Complex |
|---|---|---|---|
| 6 | 4 | 2 | 0 |
| 6 | 2 | 2 | 2 |
| 6 | 0 | 2 | 4 |
| 6 | 4 | 0 | 2 |
| 6 | 2 | 0 | 4 |
| 6 | 0 | 0 | 6 |
Notice that the positive and negative values can decrease by two independently of each other.
Rational Root Test
If a polynomial function has integer coefficients, then every rational zero will have the form p/q where p is a factor of the constant and q is a factor of the leading coefficient.
- Make sure the polynomial has integer coefficients. Multiply to get rid of fractions or decimals if need be (be sure to later divide).
- This only addresses the rational zeros. There may be real, but non-rational roots. There may be complex roots involving i.
- This says that rational zeros will have this form. It does not say that everything that has this form is a rational zero. What it does give you is a list of possible rational zeros
Example: f(x) = 4x^5 - x^2 + 12
Possible rational zeros will be of the form (factor of 12) over (factor of 4). A division table can help you find all these values
| 1 | 2 | 3 | 4 | 6 | 12 | |
|---|---|---|---|---|---|---|
| 1 | 1 | 2 | 3 | 4 | 6 | 12 |
| 2 | 1 / 2 | 1 | 3 / 2 | 2 | 3 | 6 |
| 4 | 1 / 4 | 1 / 2 | 3 / 4 | 1 | 3 / 2 | 3 |
The division table helps identify the possible rational zeros. You should throw out the duplicates, and list the others in order.
-12, -6, -4, -3, -2, -3 / 2, -1, -3 / 4, -1 / 2, -1 / 4, 1 / 4, 3 / 4, 1, 3 / 2, 2, 3, 4, 6, 12
Now, you perform synthetic division on possible rational zeros until you find one.
Here's where Descartes' Rule of Signs comes in. In this particular problem, there would be a maximum of 2 positive and 1 negative root. That means that you may have 2 or 0 positive roots, but you will always have 1 negative. There is no guarantee that negative is rational, though. Descartes only guaranteed real roots. If there were no negatives, then you would know not to try any.
Upper and Lower Bounds
If you have a polynomial with real coefficients and a positive leading coefficient, then ...
- Upper Bound
- If synthetic division is performed by dividing by x-k, where k>0, and all the signs in the bottom row of the synthetic division are non-negative, then x=k is an upper bound (nothing is larger) for the zeros of the polynomial.
- Lower Bound
- If synthetic division is performed by dividing by x-k, where k<0, and the signs in the bottom row of the synthetic division alternate (between non-negative and non-positive), then x=k is a lower bound (nothing is smaller) for the zeros of the polynomial.
The zero in the bottom row may be considered positive or negative as needed.
Suggested Attack to Finding Zeros of a Polynomial
- Identify the total number of real or complex zeros (corollary to Fundamental Theorem of Algebra).
- Identify the possible number of positive, negative, and complex zeros (Descartes' Rule of Signs).
- List the possible rational zeros (Rational Root Theorem)
- Try possible rational zeros until you find one that works. After each division by a positive value, check for possible upper bounds. After each division by a negative value, check for possible lower bounds (Upper and Lower Bound Theorems)
- After you find a possible rational root that actually works, take the quotient and continue to try to factor it until it is down to a quadratic or less. Once it is a quadratic or less, there are other ways to solve it.
- Write the linear and or linear / irreducible quadratic factorization (next section)
Really Important (and frustrating if you forget)!
Once you have found a zero using synthetic division, use the quotient as a new polynomial for all further divisions. The quotient will be one less degree than the original dividend. Each time you find a root, the quotient becomes one less in degree. Eventually, it will become a quadratic, and then you can factor, extract roots, complete the square, or use the quadratic equation to find the remaining roots.
If you continue to use the original function, you will become very frustrated and waste a lot of time.