What is the discriminant anyway?

Answer : The discriminant is a number that can be calculated from any quadratic equation

A quadratic equation is an equation that can be written as

ax ² + bx + c where a ≠ 0

What is the formula for the Discriminant?

The discriminant in a quadratic equation is found by the following formula and the discriminant provides critical information regarding the nature of the roots/solutions of any quadratic equation.

discriminant= b² − 4ac

Example of the discriminant

• Quadratic equation = y = 3x² + 9x + 5
• The discriminant = 9 ² − 4 • 3 •5

Imortant pre requisites

To understand what the discriminant does, it's important that you have a good understanding of

What a quadratic equation is:

Answer: A quadratic equation is an equation in the form of y=ax2+bx+c where ane0 Read more here on this topic

What does the graph of a quadratic equation look like:

Answer: A parabola.

What is the solution of a quadratic equation:

Answer: The solution can be thought of in two different ways.

Algebraically, the solution occurs when y = 0 . So the solution is wherey=ax2+bx+c becomes 9=ax2+bx+c

Graphically, since y = 0 is the x-axis, the solution is where the parabola intercepts the x-axis. (This only works for real solutions).
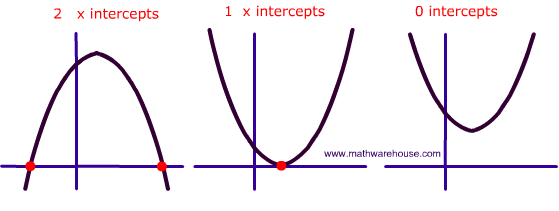
In the picture below, the left parabola has 2 real solutions (red dots), the middle parabola has 1 real solution (red dot) and the right most parabola has no real solutions (yes, it does have imaginary ones)

What does this formula tell us?

Answer: The discriminant tells us the following information about a quadratic equation:

• If the solution is a real number or an imaginary number.
• If the solution is rational or if it is irrational.
• If the solution is 1 unique number or two different numbers

Nature of the Solutions

Value of the discriminant	Type and number of Solutions	Example of graph
Positive Discriminant b² − 4ac > 0	Two Real Solutions If the discriminant is a perfect square the roots are rational. Otherwise, they areirrational.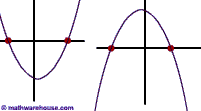
Positive and a Perfect Square b² − 4ac = perfect square	Two Real RationalSolutions.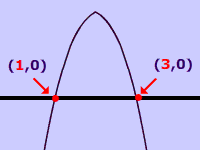
Positive and anot a perfect square b² − 4ac = not a perfect square	Two Real IrrationalSolutions.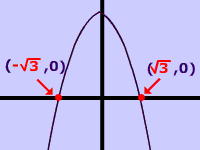
Discriminant is Zero b² − 4ac = 0	One Real Solution
Negative Discriminant b² − 4ac < 0	No Real Solutions Two ImaginarySolutions

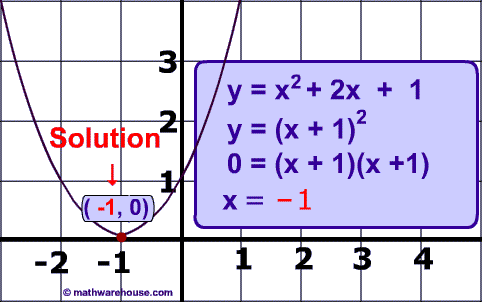
• Example 1
  Quadratic Equation: y = x² + 2x + 1
  • a = 1
  • b = 2
  • c = 1
  The discriminant for this equation is

  b2−4ac22−4(1)(1)=0 

  Since the discriminant is zero, there should be 1 real solution to this equation. Below is a picture representing the graph and one solution of this quadratic equation

  Graph of y = x² + 2x + 1