Graphing Quadratic Equations

A Quadratic Equation in Standard Form
(a, b, and c can have any value, except that a can't be 0.) 

Here is an example:

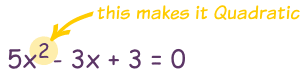
Graphing

You can graph a Quadratic Equation using our Function Grapher, but to really understand what is going on, you can make the graph yourself. Read On!

The Simplest Quadratic

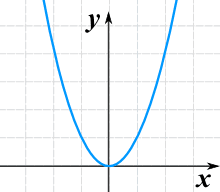
The simplest Quadratic Equation is:

f(x) = x²

And its graph is simple too:

This is the curve f(x) = x²
It is a parabola.

Now let us see what happens when we introduce the "a" value:

f(x) = ax²

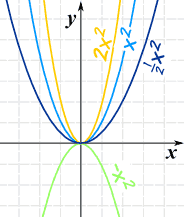
• Larger values of a squash the curve
• Smaller values of a expand it
• And negative values of a flip it upside down

Play With It Now is a good time to play with the "Quadratic Equation Explorer" so you can see what different values of a, b and c produce

The "General" Quadratic

Before graphing we rearrange the equation, from this:

f(x) = ax² + bx + c

To this:

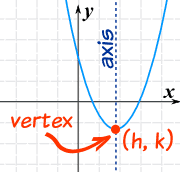
f(x) = a(x-h)² + k

Where:

h = -b/2a
k = f( h )

In other words, calculate h (=-b/2a), then find k by calculating the whole equation for x=h

First of all ... Why?

Well, the wonderful thing about this new form is that h and k show you the very lowest (or very highest) point, called the vertex: And also the curve is symmetrical (mirror image) about the axis that passes through x=h, making it easy to graph

So ...

• h shows you how far left (or right) the curve has been shifted from x=0
• k shows you how far up (or down) the curve has been shifted from y=0

Lets see an example of how to do this:

Example: Plot f(x) = 2x² - 12x + 16

First, let's note down:

• a = 2,
• b = -12, and
• c = 16

Now, what do we know?

• a is positive, so it is an "upwards" graph ("U" shaped)
• a is 2, so it is a little "squashed" compared to the x² graph

Next, let's calculate h:

h = -b/2a = -(-12)/(2x2) = 3

And next we can calculate k (using h=3):

k = f(3) = 2(3)² - 12·3 + 16 = 18-36+16 = -2

So now we can plot the graph (with real understanding!):

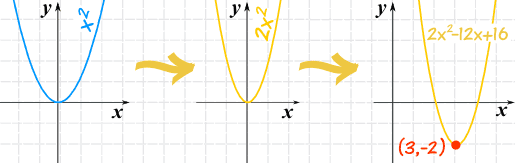
We also know: the vertex is (3,-2), and the axis is x=3

From A Graph to The Equation

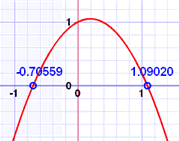
What if you have a graph, and want to find an equation?

Example: you have just plotted some interesting data, and it looks Quadratic:

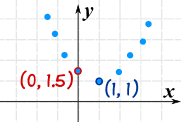
Just knowing those two points we can come up with an equation.

Firstly, we know h and k (at the vertex):

(h, k) = (1,1)

So let's put that into this form of the equation:

f(x) = a(x-h)² + k

f(x) = a(x-1)² + 1

Then we calculate "a":

We know (0, 1.5) so:		f(0) = 1.5
And we know the function (except for a):		f(0) = a(0-1)2 + 1 = 1.5
Simplify:		f(0) = a + 1 = 1.5
		a = 0.5

And so here is the resulting Quadratic Equation:

f(x) = 0.5(x-1)² + 1

Note: This may not be the correct equation for the data, but it’s a good model and the best we can come up with.