How Polynomials Behave
A polynomial looks like this: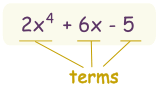 |
| example of a polynomial |
Continuous and Smooth
There are two main things about the graphs of Polynomials:
The graphs of polynomials are continuous, which is a special term with an exact definition in calculus, but here we will use this simplified definition:
 you can draw it without lifting your pen from the paper
you can draw it without lifting your pen from the paper
The graphs of polynomials are also smooth. No sharp "corners" or "cusps"
How the Curves Behave
Let us graph some polynomials to see what happens ...
... and let us start with the simplest form:
f(x) = xn
Which actually does interesting things:
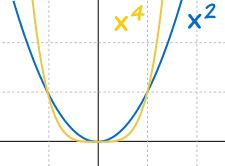 |
Even values of "n" behave the same:
|
And:
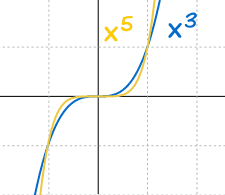 |
Odd values of "n" behave the same
|
Power Function of Degree n
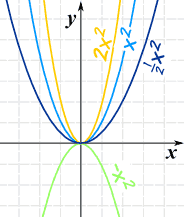
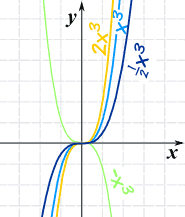
Next, by including a multiplier of a we get what is called a "Power Function":
f(x) = axn
f(x) equals a times x to the "power" (ie exponent) n
f(x) equals a times x to the "power" (ie exponent) n
The "a" changes it this way:
- Larger values of a squash the curve (inwards to y-axis)
- Smaller values of a expand it (away from y-axis)
- And negative values of a flip it upside down
| Example: f(x) = ax2 a = 2, 1, ½, -1 | Example: f(x) = ax3 a = 2, 1, ½, -1 |
 |  |
We can use that knowledge when sketching some polynomials:
Example: Make a Sketch of y=1-2x7
Start with the simplest "odd power" graph of x3, and gradually turn it into 1-2x7
- You know how x3 looks,
- x7 will be similar, but flatter near zero, and steeper elsewhere,
- Squash it to get 2x7,
- Flip it to get -2x7, and
- Raise it by 1 to get 1-2x7.
Like this:
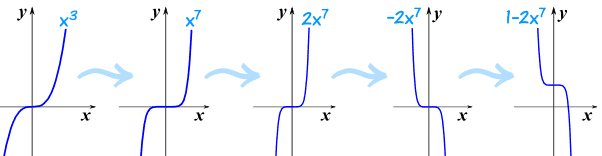
So by doing this step-by-step we can get a good result.
Turning Points
A Turning Point is an x-value where a local maximum or local minimum happens:
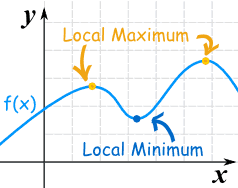
How many turning points does a polynomial have?
Never more than the Degree minus 1
The Degree of a Polynomial with one variable is the largest exponent of that variable.
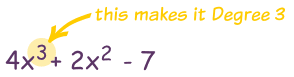
Example: a polynomial of Degree 4 will have 3 turning points or less
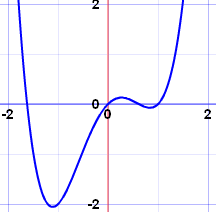 | 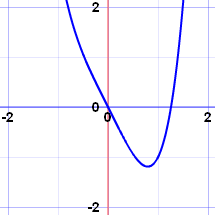 | |
| x4-2x2+xhas 3 turning points | x4-2xhas only 1 turning point |
The most is 3, but there can be less.
You may not know where they are, but at least you know the most there can be!
What Happens at the Ends
And when you move far from zero:
- far to the right (large values of x), or
- far to the left (large negative values of x)
then the graph starts to resemble the graph of y = axn where axn is the term with the highest degree.
Example: f(x) = 3x3-4x2+x
Far to the left or right, the graph will look like 3x3
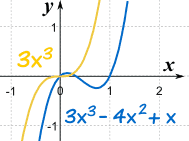 | 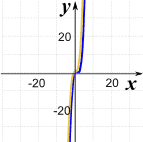 | |
| Near Zero, they are different | Far From Zero, they become similar |
This makes sense, because when x is large, then x3 is much greater than x2 etc
This is officially called the "End Behavior Model".
And yes, we have come to the end!
Summary
- Graphs will be continuous and smooth
- Even exponents behave the same: above (or equal to) 0; go through (0,0), (1,1) and (-1,1); larger values of n flatten out near 0, and rise more sharply.
- Odd exponents behave the same: go from negative x and y to positive x and y; go through (0,0), (1,1) and (-1,-1); larger values of n flatten out near 0, and fall/rise more sharply
- Factors:
- Larger values squash the curve (inwards to y-axis)
- Smaller values expand it (away from y-axis)
- And negative values flip it upside down
- Turning points: there will be "Degree-1" or less.
- End Behavior: use the term with the largest exponent
Factors and Roots of a Polynomial Equation
Here are three important theorems relating to the roots of a polynomial:(a) A polynomial of n-th degree can be factored into n linear factors.(b) A polynomial equation of degree n has exactly n roots.(c) If(x−r) is a factor of a polynomial, thenx=r is a root of the associated polynomial equation.Let's look at some examples to see what this means.Example 1
The cubic polynomial f(x) = 4x3 − 3x2 − 25x − 6 has degree3 (since the highest power of x that appears is3 ).This polynomial can be factored (using Scientific Notebook or similar software) and written as4x3 − 3x2 − 25x − 6 = (x − 3)(4x + 1)(x + 2)So we see that a 3rd degree polynomial has 3 roots.The associated polynomial equation is formed by setting the polynomial equal to zero:f(x) = 4x3 − 3x2 − 25x − 6 = 0
In factored form, this is:(x−3)(4x+1)(x+2)=0 We see from the expressions in brackets and using the 3rd theorem from above, that there are 3 roots,x=3 ,−14 ,−2 .In this example, all 3 roots of our polynomial equation of degree 3 are real.Since(x−3) is a factor, thenx=3 is a root.Since(4x+1) is a factor, thenx=−14 is a root.Since(x+2) is a factor, thenx=−2 is a root.Example 2
The equationx5 − 4x4 − 7x3 + 14x2 − 44x + 120 = 0 can be factored (using Scientific Notebook) and written as:(x − 2)(x − 5)(x + 3)(x2 + 4) = 0
We see there are 3 real rootsx=2,5,−3, and 2complex rootsx=±2j , (wherej=−1−−−√ ).So our 5th degree equation has 5 roots altogether.[Do you need revision on complex numbers? Go toComplex Numbers.]Example 3
In the previous section, Remainder Theorem and the Factor Theorem, we found in one of the examples that (x + 1) is a factor of f(x) = x3 + 2x2 − 5x − 6.This means thatx=−1 is a root ofx3+2x2−5x−6=0 .[To check this, substitutex=−1 into the polynomial. If it is a root, then you should get value0 when you substitute.]Example 4
The following polynomial equation would be rather tricky to solve using the Remainder and Factor Theorems. We will solve it using Scientific Notebook:x4 + 0.4x3 − 6.49x2 + 7.244x − 2.112 = 0
Note: Polynomial equations do not always have "nice" solutions! (By "nice solutions" I mean solutions which are integers or simple fractions.) This is why I feel the Remainder and Factor Theorems are pretty useless, because you can only use them if at least some of the solutions are integers or simple fractions.If you use a computer algebra system (like Wolfram | Alpha or Scientific Notebook) to solve these, you can be done in seconds and move on to something more meaningful, like the applications.Example 5
Solve the following polynomial equation using Scientific Notebook:3x3 − x2 − x + 4 = 0.
Using LiveMath to find Roots
We can also use LiveMath (or any similar Computer Algebra System) to find roots. This can be done graphically OR using the in-built root-finder.Using a graph in LiveMath, we can easily find the roots ofx5 + 8.5x4 + 10x3 − 37.5x2 − 36x + 54 = 0.since the roots are the x-intercepts (i.e. where the function has value0 ).Let's see this how to do this in LiveMath:Complex Roots
Regarding complex roots, the following theorem applies :If the coefficients of the equation
f(x)=0 are real anda+bj is a complex root, then its conjugatea−bj is also a root.For more on complex numbers, see: Complex NumbersExample 6
In Example (2) above, we had 3 real roots and 2 complex roots. Those complex roots form a complex conjugate pair,x = 0 − 2j and x = 0 + 2j
Example 7
The factors of the polynomial x3+ 7x2 + 17x + 15 are found using LiveMath:x3 + 7x2 + 17x + 15 = (x + 3)(x + 2 − j)(x + 2 + j)So the roots arex=−3
x=−2+j andx=−2−j There is one real root and the remaining 2 roots form a complex conjugate pair.Remainder Theorem
and Factor TheoremOr: how to avoid Polynomial Long Division when finding factorsDo you remember doing division in Arithmetic?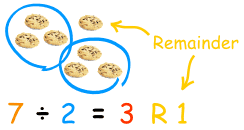 "7 divided by 2 equals 3 with a remainder of 1"Each part of the division has names:
"7 divided by 2 equals 3 with a remainder of 1"Each part of the division has names: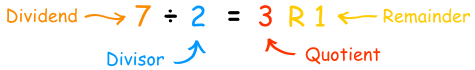 Which can be rewritten as a sum like this:
Which can be rewritten as a sum like this: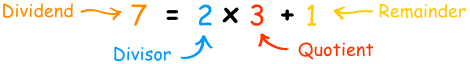
Polynomials
Well, we can also divide polynomials.f(x) ÷ g(x) = q(x) with a remainder of r(x)But it is better to write it as a sum like this: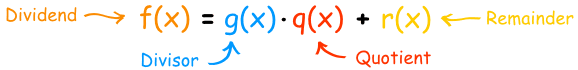 I can show you this in an example using Polynomial Long Division:
I can show you this in an example using Polynomial Long Division:Example: 2x2-5x-1 divided by x-3
- f(x) is 2x2-5x-1
- g(x) is x-3
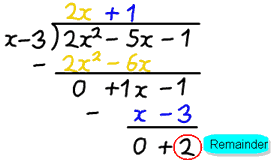 After dividing we get the answer 2x+1, but there is a remainder of 2.
After dividing we get the answer 2x+1, but there is a remainder of 2.- q(x) is 2x+1
- r(x) is 2
In the style f(x) = g(x)·q(x) + r(x) we can write:2x2-5x-1 = (x-3)(2x+1) + 2But you need to know one more thing:When you divide by a polynomial of degree 1 (such as "x-3") the remainder will have degree 0(in other words a constant, like "4").And we are going to use that idea in the "Remainder Theorem":The Remainder Theorem
When you divide a polynomial f(x) by x-c you get:f(x) = (x-c)·q(x) + r(x)But r(x) is simply the constant r (remember? when you divide by (x-c) the remainder is a constant) .... so we get this:f(x) = (x-c)·q(x) + rNow see what happens when you have x equal to c:f(c) = (c-c)·q(c) + rf(c) = (0)·q(c) + rf(c) = rSo we get this:The Remainder Theorem:When you divide a polynomial f(x) by x-c the remainder r will be f(c)So if you want to know the remainder after dividing by x-c you don't need to do any division:Just calculate f(c).Let us see that in practice:Example: 2x2-5x-1 divided by x-3
(Continuing our example from above)We don't need to divide by (x-3) ... just calculate f(3):2(3)2-5(3)-1 = 2x9-5x3-1 = 18-15-1 = 2And that is the remainder we got from our calculations above.We didn't need to do Long Division at all!Example: Dividing by x-4
(Continuing our examplee)What would the remainder be if we divided by "x-4" ?"c" is 4, so let us check f(4):2(4)2-5(4)-1 = 2x16-5x4-1 = 32-20-1 = 11Once again ... We didn't need to do Long Division to find it.The Factor Theorem
Now ...What if you calculated f(c) and it was 0?... that means the remainder is 0, and ...... (x-c) must be a factor of the polynomial!Example: x2-3x-4
f(4) = (4)2-3(4)-4 = 16-12-4 = 0so (x-4) must be a factor of x2-3x-4And so we have:The Factor Theorem:When f(c)=0 then x-c is a factor of the polynomialAnd the other way around, too:When x-c is a factor of the polynomial then f(c)=0Why Is This Useful?
Knowing that x-c is a factor is the same as knowing that c is a root (and vice versa).The factor "x-c" and the root "c" are the same thingKnow one and you know the otherFor one thing, it means that you can quickly check if (x-c) is a factor of the polynomial.Example: 2x3-x2-7x+2
The polynomial is degree 3, and could be difficult to solve. So let us plot it first: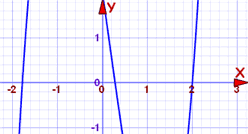 The curve crosses the x-axis at three points, and one of them might be at 2. We can check easily:f(2) = 2(2)3-(2)2-7(2)+2 = 16-4-14+2 = 0Yes! f(2)=0, so we have found a root and a factor.So (x-2) must be a factor of 2x3-x2-7x+2How about where it crosses near -1.8?f(-1.8) = 2(-1.8)3-(-1.8)2-7(-1.8)+2 = -11.664-3.24+12.6+2 = -0.304No. (x+1.8) is not a factor.
The curve crosses the x-axis at three points, and one of them might be at 2. We can check easily:f(2) = 2(2)3-(2)2-7(2)+2 = 16-4-14+2 = 0Yes! f(2)=0, so we have found a root and a factor.So (x-2) must be a factor of 2x3-x2-7x+2How about where it crosses near -1.8?f(-1.8) = 2(-1.8)3-(-1.8)2-7(-1.8)+2 = -11.664-3.24+12.6+2 = -0.304No. (x+1.8) is not a factor.Summary
The Remainder Theorem:- When you divide a polynomial f(x) by x-c the remainder will be f(c)
The Factor Theorem:- When f(c)=0 then x-c is a factor of the polynomial
- When x-c is a factor of the polynomial then f(c)=0
The Rational Zeros Theorem
Roots of a Polynomial
A root or zero of a function is a number that, when plugged in for the variable, makes the function equal to zero. Thus, the roots of a polynomial P(x) are values of x such that P(x) = 0 .The Rational Zeros Theorem
The Rational Zeros Theorem states:If P(x) is a polynomial with integer coefficients and if
 is a zero of P(x) (P(
is a zero of P(x) (P( ) = 0 ), then p is a factor of the constant term of P(x)and q is a factor of the leading coefficient of P(x) .We can use the Rational Zeros Theorem to find all the rational zeros of a polynomial. Here are the steps:
) = 0 ), then p is a factor of the constant term of P(x)and q is a factor of the leading coefficient of P(x) .We can use the Rational Zeros Theorem to find all the rational zeros of a polynomial. Here are the steps:- Arrange the polynomial in descending order
- Write down all the factors of the constant term. These are all the possible values of p .
- Write down all the factors of the leading coefficient. These are all the possible values of q .
- Write down all the possible values of
 . Remember that since factors can be negative,
. Remember that since factors can be negative,  and -
and -  must both be included. Simplify each value and cross out any duplicates.
must both be included. Simplify each value and cross out any duplicates. - Use synthetic division to determine the values of
 for which P(
for which P( ) = 0 . These are all the rational roots of P(x) .
) = 0 . These are all the rational roots of P(x) .
Example: Find all the rational zeros of P(x) = x 3 -9x + 9 + 2x 4 -19x 2 .- P(x) = 2x 4 + x 3 -19x 2 - 9x + 9
- Factors of constant term: ±1 , ±3 , ±9 .
- Factors of leading coefficient: ±1 , ±2 .
- Possible values of
 : ±
: ±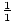 , ±
, ±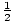 , ±
, ±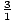 , ±
, ±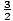 , ±
, ±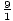 , ±
, ±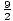 . These can be simplified to: ±1 , ±
. These can be simplified to: ±1 , ±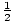 , ±3 , ±
, ±3 , ±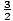 , ±9 , ±
, ±9 , ±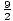 .
. - Use synthetic division:
Thus, the rational roots of P(x) are x = - 3 , -1 ,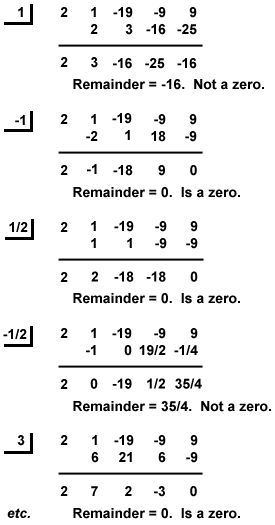 Figure %: Synthetic Division
Figure %: Synthetic Division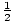 , and 3 .We can often use the rational zeros theorem to factor a polynomial. Using synthetic division, we can find one real root a and we can find the quotient when P(x) is divided by x - a . Next, we can use synthetic division to find one factor of the quotient. We can continue this process until the polynomial has been completely factored.
, and 3 .We can often use the rational zeros theorem to factor a polynomial. Using synthetic division, we can find one real root a and we can find the quotient when P(x) is divided by x - a . Next, we can use synthetic division to find one factor of the quotient. We can continue this process until the polynomial has been completely factored.
Example (as above): Factor P(x) = 2x 4 + x 3 -19x 2 - 9x + 9 .
As seen from the second synthetic division above, 2x 4 + x 3 -19x 2 -9x + 9÷x+ 1 = 2x 3 - x 2 - 18x + 9 . Thus, P(x) = (x + 1)(2x 3 - x 2 - 18x + 9) . The second term can be divided synthetically by x + 3 to yield 2x 2 - 7x + 3 . Thus, P(x) = (x+ 1)(x + 3)(2x 2 - 7x + 3) . The trinomial can then be factored into (x - 3)(2x - 1). Thus, P(x) = (x + 1)(x + 3)(x - 3)(2x - 1) . We can see that this solution is correct because the four rational roots found above are zeros of our result.
No comments:
Post a Comment