Descartes' Sign Rule

A method of determining the maximum number of positive and negative real roots of a polynomial.

For positive roots, start with the sign of the coefficient of the lowest (or highest) power. Count the number of sign changes 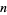 as you proceed from the lowest to the highest power (ignoring powers which do not appear). Then  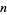is the maximum number of positive roots. Furthermore, the number of allowable roots is 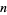, , 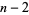, 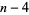.... For example, consider the polynomial

(1)

Since there are three sign changes, there are a maximum of three possible positive roots.

For negative roots, starting with a polynomial 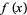, write a new polynomial  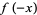with the signs of all odd powers reversed, while leaving the signs of the even powers unchanged. Then proceed as before to count the number of sign changes 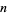. Then  is the maximum number of negative roots. For example, consider the polynomial

(2)

and compute the new polynomial

(3)

In this example, there are four sign changes, so there are a maximum of four negative roots.

Intermediate Value Theorem

The idea behind the Intermediate Value Theorem is this:

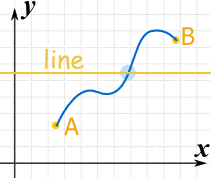When you have two points connected by a continuous curve: one point below the line the other point above the line ... then there will be at least one place where the curve crosses the line!

Well of course you must cross the line to get from A to B!

Now that you know the idea, let's look more closely at the details.

Continuous

The curve must be continuous ... no gaps or jumps in it.

"Continuous" is a special term with an exact definition in calculus, but here we will use this simplified definition:

you can draw it without lifting your pen from the paper

More Formal

Here is that idea stated more formally:

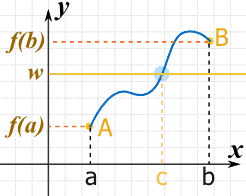		When: The curve is the function y = f(x), which is continuous on the interval [a, b], and w is a number between f(a) and f(b),
		Then ...

... there must be at least one value c within [a, b] such that f(c) = w

In other words the function y = f(x) at some point must be w = f(c)

Notice that:

• w is between f(a) and f(b), which leads to ...
• c must be between a and b

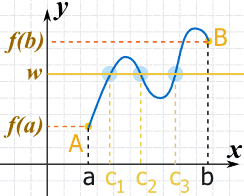
At Least One It also says "at least one value c", which means you could have more. Here, for example, are 3 points where f(x)=w.